Static analysis tools comparisons

It is very easy to make snap judgments about other static analyzers when you are yourself working on one. You do not even need to act in bad faith: you just try the other tools on the programs that you worked hard to give interesting results on — difficult examples, on which even your own tool does not give the best result. You intend to give the other tool a passing grade if it produces a result as approximated as yours, and to acknowledge that it's not as bad as you thought if it gives a better result.

The flaw in this line of reasoning is that even if you were honest enough to pick an example on which it was possible to improve on your own tool's result, you picked one on which your tool begins to produce a result. The example is automatically in the language subset that your analyzer handles, probably in the language subset it targets. The comparison is still heavily biased in favor of your tool, whether you realize it or not. This is how you may end up thinking that Frama-C's value analysis only manipulates intervals: by only trying it on programs for which it displays intervals (programs, say, translated to C from this toy language).

Astrée

It is more instructive to take examples from other tools' websites the examples that they use to advertise and to see what your own tool can do with them. Let us do this in this post.

Feeling lucky?

Here is one:

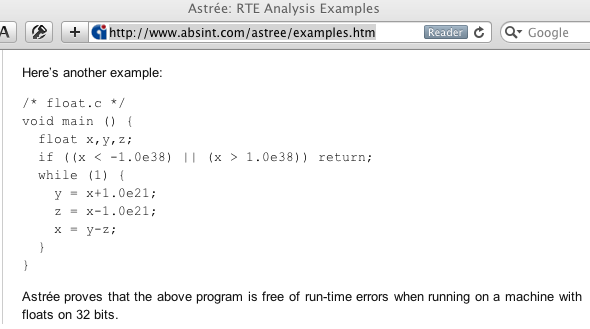
Let's try it in Frama-C's value analysis:

$ bin/toplevel.opt -val astree.c
[kernel] preprocessing with "gcc -C -E -I.  astree.c"
astree.c:4: Floating-point constant 1.0e38 is not represented exactly.
     Will use 0x1.2ced32a16a1b1p126. See documentation for option -warn-decimal-float
...
astree.c:4: accessing uninitialized left-value: assert \initialized(&x);
astree.c:4: completely undefined value in {{ x -> {0} }} (size:<32>).
...
[value] Values at end of function main:
          NON TERMINATING FUNCTION

The webpage adds: "Astrée proves that the above program is free of run-time errors when running on a machine with floats on 32 bits." That's reassuring. If we had not read that we might have feared that it contained undefined behavior due to the use of uninitialized variable x (and perhaps others but really there is such a big problem with x that the value analysis did not look any further). "Undefined behavior" means that anything can happen and you should consider yourself lucky if it's a run-time error. With an uninitialized float variable you just might be lucky (and get a run-time error instead of the proverbial demons flying out of your nose): the compiler may produce code that reads bits from the stack that happen to represent a signaling NaN and then applies a floating-point operation to it causing a run-time error.

Miscommunication

To be fair the release notes for the latest version of Astrée said that it could now emit alarms for uninitialized variables. I look forward to an example illustrating that. Perhaps that example will demonstrate an unsoundness in Frama-C's value analysis who knows?

Also the sentence "Astrée proves that the above program is free of run-time errors…" really means "Astrée does not find any of the run-time errors that it detects in the above program" and both its designers and its users at Airbus Operations S.A. are aware of this meaning. It's just that the somewhat pompous formulation is a little bit unfortunate on this example.

Coincidentally I sometimes notice the same phrase used about "Frama-C" this time by makers of comparable tools as below:

Frama-C "proves" [something ridiculous] about [this program].

It's usually just another instance of someone running other tools on the examples eir tool is good at of course and might more objectively be phrased as:

An external plug-in of Frama-C separately distributed written by a PhD student so brilliant that he was able to produce useful software during his PhD in addition to making several solid contributions to the science of program analysis "proves" [something ridiculous] about [a program that's out of scope for this plug-in].

It doesn't have the same ring to it. I see why toolmakers prefer to peddle their own imperfect creations using the first sentence.

Polyspace

So many rhetorical questions

Polyspace's website has this example:

On the webpage the explanation of why this example is interesting is a little confusing:

Now rounding is not the same when casting a constant to a float or a constant to a double:

* floats are rounded to the nearest lower value;

* doubles are rounded to the nearest higher value;

Now are they really? Floating-point has an aura of arbitrariness about it but that would be a little bit over the top wouldn't it? Isn't it just that the number 3.40282347e+38 when rounded to float in round-to-nearest mode rounds downwards and when rounded to double in round-to-nearest mode rounds upwards?

Letting the compiler be the judge

According to the colored comments in the program Polyspace guarantees that there is an overflow. Well let's try it then:

$ bin/toplevel.opt -val ps_ovfl.c -warn-decimal-float all -float-hex
...
ps_ovfl.c:4: Floating-point constant 3.40282347e+38f is not represented exactly.
     Will use 0x1.fffffe0000000p127
ps_ovfl.c:5: Floating-point constant 3.40282347e+38 is not represented exactly.
     Will use 0x1.fffffe091ff3dp127
...
[value] Values at end of function main:
          x ∈ 0x1.fffffe0000000p127
          y ∈ 0x1.fffffe0000000p127

Frama-C's value analysis does not agree about the example. Ah but this is about floating-point subtleties. It's not a cut-and-dry case of uninitialized variable. Perhaps Polyspace is right. However we may remember that in floating-point an overflow is not a run-time error: it produces an infinity a special kind of value that some numerical algorithms handle correctly but most don't. It makes sense for a static analyzer to treat infinities as errors (in fact the value analysis does too) but if a static analyzer says that an overflow certainly occurs(red alarm) and we are unsure of this diagnostic we can run the program and see what happens. It's not undefined in the C sense.

#include <stdio.h>
void main(void)
{
    float x  y;
    x = 3.40282347e+38f; // is green
    y = (float) 3.40282347e+38; // OVFL red
    printf("%a %a %d"  x  y  x == y);
}

$ gcc ps_ovfl_modified.c
...
~/ppc $ ./a.out
0x1.fffffep+127 0x1.fffffep+127 1

No no overflow it seems. Polyspace's red alarm led us to expect the output 0x1.fffffep+127 inf 0 but that's not what happens.

An explanation why Polyspace makers think there should be an overflow

The explanation on the webpage continues:

In the case of the second assignment the value is cast to a double first - by your compiler using a temporary variable D1 - then into a float - another temporary variable - because of the cast. Float value is greater than MAXFLOAT so the check is red.

Unfortunately this not how round-to-nearest works. When a double here 0x1.fffffe091ff3dp127 falls between two floats here 0x1.fffffep127 (MAXFLOAT) and +infinity the nearest one should be picked.

A philosophical conundrum

Which is nearest between a finite float and an infinite one? I would like to recommend this question for the next philosophy A-levels (or equivalent worldwide). In the world of IEEE 754 the answer is terribly pragmatic. Infinity starts at the first number in floating-point format that can't be represented for having too high an exponent. For single-precision this number is 0x1.0p128. The midpoint between this unrepresentable number and the last finite float 0x1.fffffep127 is 0x1.ffffffp127 and therefore in round-to-nearest all numbers above 0x1.ffffffp127 round up to +inf whereas numbers below 0x1.ffffffp127 round down to 0x1.fffffep127.

Experimentation

The number 0x1.ffffffp127 is representable as a double so that we can obtain a decimal approximation of it with a simple C program:

#include <stdio.h>
main(){
  printf("%.16e"  0x1.ffffffp127);
}
$ gcc limit.c
$ ./a.out
3.4028235677973366e+38

My claim is that regardless of what Polyspace's website says and although the number 3.402823567797336e+38 is much larger than the number in their example you can round it to a double and then to a float and you will still get the finite 0x1.fffffep127 (MAXFLOAT). Conversely the number 3.402823567797337e+38 is on the other side of the fence and rounds to +inf.

We can try it out:

#include <stdio.h>
main(){
  printf("%a %a"  (float) 3.402823567797336e+38   (float) 3.402823567797337e+38);
}
$ gcc experiment1.c
$ ./a.out
0x1.fffffep+127 inf

What about the number 3.4028235677973366e+38? It is even more amusing. It is below the fence and converted directly to float it gives 0x1.fffffep127. However converted to double it rounds to 0x1.ffffffp127. Then when rounding to float the "even" rule for picking between two equidistant floats results in 0x1.0p128 being picked and the final float result is therefore +inf.

#include <stdio.h>
main(){
  printf("%a %a"  3.4028235677973366e+38f  (float) 3.402823567797366e+38);
}
$ gcc experiment2.c
$ ./a.out
0x1.fffffep+127 inf

This is a case of double rounding just like in question 5 here.

But really Polyspace wouldn't be that wrong would it?

I'm afraid it would. Unlike the webpage on Astrée's site I cannot find any plausible explanation for the misunderstanding. The example is wrong and the explanations that follow make it worse. It could be the case that Polyspace gives results that cover all possible floating-point rounding modes just like the value analysis option -all-rounding-modes does. There would be an overflow then (in round-upwards mode). Unfortunately Polyspace would have to emit an orange since in round-to-nearest and in round-downwards there is no overflow. It would have to produce results similar to those below predicting that either the overflow or the normal termination of the program can happen.

$ bin/toplevel.opt -val ps_ovfl.c -all-rounding-modes -float-hex
...
ps_ovfl.c:5:[kernel] warning: overflow in float (0x1.fffffe091ff3dp127).
                  assert -0x1.fffffe0000000p127f ≤ (float)3.40282347e+38 ∧
                  (float)3.40282347e+38 ≤ 0x1.fffffe0000000p127f;
...
[value] Values at end of function main:
          x ∈ 0x1.fffffe0000000p127
          y ∈ 0x1.fffffe0000000p127

Conclusion

In conclusion we should be careful about the way we express ourselves: static analysis has been oversold enough already. We would do well to learn the rules we pretend to enforce and we should avoid picking on other toolmakers something which is detrimental for all and that I do not completely avoid in this post. However I use each tool's own example which I think is a good sign that there is still some major overselling going on despite how detrimental this has already been in the past. I would tell you about examples on PVS-Studio's website but at least it has different goals and does not use the verb "prove" in the sense "my imperfect implementation based on an idealized formalization computes that…" all the time.